Salut tout le monde, ce soir je vais vous présenter une étude statistique que j'ai menée pendant 4 ans et demi pour payer le moins cher possible lorsque je prends le bus
j'ai essayé d'aerer mon texte et de l'illustrer, si ca vous plait pas lisez au moins les trucs en gras qui attirent l'oeil

ici le prix du bus est de deux euros 10 et le chauffeur est normalement tenu de me laisser passer qu'importe la situation, si jamais je passe sans payer et qu'il est au courant, c'est lui qui est en faute (etant donné que ce sont des bus scolaires que je squattte c'est pas les mêmes regles que pour les bus des transports en commun

on va partir de l'idée suivante quand on donne un gros billet au chauffeur, il a parfois tellement la flemme de rendre la monnaie qu'il préfere vous laisser passer gratos mais pas toujours

et nous avons les deux contraites suivantes
(1) le chauffeur peut quand meme vous prendre votre gros billet et vous faire payer, tout dépend du billet présenté
(2) le chauffeur va plus ou moins en avoir sa claque de vous faire crédit pendant plusieurs jours et il refusera de vous faire monter a partir d'un certain seuil d'agacement

l'objectif de cette étude est de savoir quel est le billet a présenter au chauffeur pour avoir un maximum de chances de passer sans payer et sans etre refusé pendant un maximum de temps

étudions la contrainte (1)
pendant un certain temps j'ai présenté a chaque chauffeur de bus un billet de 20 euros , de 10 euros, de 5 euros, deux piéces de 2 euros, et 3 euros en piéces. et j'ai calculé a chaque fois la probabilité qu'il accepte le billet, et j'obtiens ceci :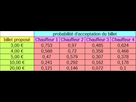
c'est a dire que par exemple le premier chauffeur a 75,3% de chances de ne pas me laisser passer gratuitement si je lui présente 3 euros
il semblerait que l'acceptation du billet par le chauffeur soit inversement proportionnelle au montant proposé ( ce qui est logique, avec un billet de 20 il va avoir plutot tendance a vous laisser passer qu'avec 3 euros )
je vais donc modéliser graphiquement l'inverse de la probabilité d'acceptation de chaque chauffeur en fonction du prix, et on obtient ceci :
il semblerait qu'il y ait une corrélation lineaire qui fait correspondre ces deux variables pour chaque chauffeur, c'est a dire une equation lineaire de type Y=A*X avec X=1/P, P etant le montant du billet proposé et p la probabilité d'echec
considérons Ø le coefficient directeur de chacune de ces fonctions linéaires, qu'on nommera coefficient de flemme
je calcule, en négligeant l'incertitude, le coefficient de flemme moyen Ø pour chacun des chauffeurs ,
j'obtiens respectivement Ø = 2.4; 2.9; 1.5 et 1.8 pour les chauffeurs étudiés
et la formule faisant correspondre la probabilité d'echec avec le montant proposé se calcule ainsi par la relation p=Ø/P
P le montant, p la probabilité d'echec ( c'est a dire de ne pas passer gratuitement ) , P le montant proposé au chauffeur,Ø le coefficient de flemme

étudions maintenant la contrainte (2)
comme je vous disais, le chauffeur peut refuser de nous faire monter car il sait qu'on se fout de sa gueule, j'ai donc relevé le temps moyen( en jours ) qu'il faut pour que chaque chauffeur refuse de me me laisser monter en fonction du billet grace auquel j'ai grugé :

par exemple le chauffeur 2 va me laisser monter en moyenne 2.7 jours avant de me refuser, et pendant ces 2,7 jours j'ai reussi a passer gratos en lui tendant un billet de 10 euros hap:
la encore il semblerait qu'il y ait une proportionnalité inverse entre le montant du billet et le nombre de jours avant le refus, comme tout a l'heure je fais une modelisation graphique :

la, pareil que tout a l'heure, une loi de la forme Y=AX, X=1/montant, semble evidente, calculons maintenant le coefficient directeur de ces droites, noté ß, que nous nommerons le coefficient de refus
je trouve pour chaque chauffeur, ß= 10, 12, 6.25, et 7.5
et nous pouvons établir la relation suivante T = ß / P, T le temps avant refus en jour, P le montant du billet

mais avant de poursuivre, je fais remarquer quelque chose, j'ai représenté graphiquement le coefficient de refus en fonction du coefficient de flemme et j'ai obtenu ceci :

le coef de refus semble dépendre du coefficient de flemme par une loi de la forme ß = Ø * µ +C
je calcule µ le coefficient directeur moyen, que je nomme l'indice de frustration, indépendant du chauffeur, egal a 2.31
et je determine l'ordonnée a l'origine C, que je nomme constante d’énervement, qui vaut 6,11
donc je conclus que ß = Ø * 2.31 + 6.11

faisons le point
nous avons determiné 3 relations :
1:d) p = Ø / P
2:d) T = ß / P soit T = ( Ø * µ +C ) /P
3:d) ß = Ø * µ +C
et nous voulons savoir quel est le billet le plus judicieux a présenter pour avoir un maximum de chances de passer sans payer et sans etre refusé
il faut donc mettre sur un seul graphique le temps avant refus en fonction du montant proposé ( T = f(P) )
ainsi que la probabilité de réussir a passer gratuitement en fonction du montant proposé, (probabilité inverse de p, on l'apelle donc p ' telle que 1-p' = p
donc on ajoute la relation '4 1-p'= Ø / P soit p' = 1 - Ø / P
mais on ne va pas comparer une probabilité ( ou un pourcentage ) avec un temps, ca n'a pas de sens, du coup on ne va pas prendre T mais un pourcentage qui lui est associé, je pose Tmax le temps maximal sans refus, que j'estime a 13 jours, il en découle donc pt = T/Tmax le pourcentage de temps sans refus par rapport au temps maximal
donc pt = (( Ø * µ +C ) /P)Tmax soit pt = ( Ø * µ +C ) /(PTmax)

représentons donc sur un graphe pt et p' en fonction de P

( a vous de fixer la valeur du coefficient de flemme, vous prenez un billet de P euros , vous le présentez a N reprises a un chauffeur, vous regardez le nombre de jours M ou il vous a quand même fait payer sans vous laisser passer gratuitement, vous calculer p = M/M et vous vous servez de la relation p = Ø / P pour trouver votre coef de flemme Ø )
j'obtiens ces courbes
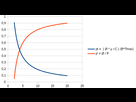
la valeur optimale du montant est celle pour laquelle se croisent les deux courbes, graphiquement elle vaut trés exactement 3.97 euros, le montant le plus proche est celui de deux piéces de 2 euros

CONCLUSION si vous donnez a chaque fois que vous prenez le bus, deux piéces de2 euros au chauffeur, celui ci a plus de chance de vous laisser passer gratuitement ( d'une part parce qu'il a la flemme de vous rendre la monnaie, d'autre part parce qu'il ne risque pas de s'enerver et de vous refuser votre argent au bout de quelques jours )

( ou alors vous lui donnez un chéque de 3.97 euros pour bien lui péter les couilles )

voila, de rien

plagie

"ce soir" ?
Non je rigole j'ai déjà vu ton topic hier soir mais j'avais la flemme de lire donc je vais le faire maintenant

Le 09 septembre 2015 à 17:11:07 UltraSaiyan a écrit :
plagie

bravo je me suis auto plagié kom c grav

Mdr g pa lu.

First paj

Le 09 septembre 2015 à 17:11:39 MainCeleste a écrit :
"ce soir" ?
Non je rigole j'ai déjà vu ton topic hier soir mais j'avais la flemme de lire donc je vais le faire maintenant

oui je comprends, c'est pour ca que je le reposte, avec quelques modifications

C/c de cette nuit

Le 09 septembre 2015 à 17:13:15 Saden_Hussein a écrit :
C/c de cette nuit

ouais je sais, j'aurais pas du le poster cette nuit

putain c'est quoi ce bordel mathématique ?

Ça me paraît étonnant que le chauffeur est la flemme de rendre pour 3e .

• ait.

Bordel d'illetré que je suis .

Le 09 septembre 2015 à 17:14:38 Ediboss a écrit :
putain c'est quoi ce bordel mathématique ?

tout est juste, verifie

Le 09 septembre 2015 à 17:14:43 Danaby a écrit :
Ça me paraît étonnant que le chauffeur est la flemme de rendre pour 3e .

ah si, le mec si tu lui file pas exactement le prix exact il te grogne " oh c'est bon passe "

Gpalu lol

L'auteur Moi je lui dit pour l'instant que ma carte est en cours de validation etant donné ma commune
Quand au 20€ le chauffeur les accepte ou me refuse l'acces au bus

Le 09 septembre 2015 à 17:16:49 Rockstarkiller a écrit :
L'auteur Moi je lui dit pour l'instant que ma carte est en cours de validation etant donné ma commune
Quand au 20€ le chauffeur les accepte ou me refuse l'acces au bus

ah mais le coup de la carte ca marche 2 jours et il péte un cable aprés
il accepte les 20 euros ? on peut considerer qu'il a un coefficient de flemme completement nul

Mdr Abra t'es un taré.

J'ai tout lu

Le 09 septembre 2015 à 17:20:15 DaJunikii a écrit :
J'ai tout lu

et qu'en penses tu ?